三角形 の 証明 234212-三角形の証明 導入

 ヘロンの公式の図解 Step① 内接円の性質から S = s r Step② s − a, s − b, s − c を見つける Step③ A P ′ = s を示す Step④ A P O と A P ′ O の相似 Step⑤ C O P と O ′ C P ′ の相似 Step⑥ (1), (2), (3) を解く 三角関数を用いた証明 公式の証明方法 ①ベクトル表示の証明 ②成分表示の証明 ベクトルによる三角形の面積の計算問題 計算問題①「大きさと内積から求める」 計算問題②「原点を頂点にもつ三角形」 計算問題③「頂点の座標から求める」3内部にできる6つの三角形は面積が等しい の証明 中線によって，三角形は面積の等しい2つの三角形に分割されます。 さらに，下の図のように各頂点と重心を結ぶ3直線によって，三角形は面積の等しい3つの三角形に分割されます。

世界に一つだけの 三角形ペア 発見 慶大院生２人証明 朝日新聞デジタル

三角形の証明 導入

三角形の証明 導入-三角形の合同の証明① 下の図で，ab=ac，−bad=−cad である。このとき，¼abd×¼acd で あることを右のように証明した。下線部 をうめて，証明を完成させなさい。 三角形の合同の証明② 下の図で，am=cm，bm=dm であ る。このとき，ab=cd であることを右9/2/ 公式の証明 このように、三角形の内接円の半径を求める問題で、公式 \(S= \frac{1}{2}r(abc)\) が大活躍します。 「内接円の半径」ときたら、ほぼこの公式一択といってもいい

Studydoctor三角形の合同の証明 応用 中２数学 Studydoctor

三角形の形状・証明問題 例 次の等式が成り立つとき，この ABCはどんな形の三角形か． a sin A=b sin sin C (答案) などを代入すると， これより，a2＝b2＋c2 ∠A＝90゜の直角三角形・・・ (答) 最後の詰めは，どうするのか9/9/19 「三角形の内角の和が180度である」ことを用いると、 「四角形の内角の和が360度である」 ことを証明できます。 また、これをしっかり理解できると、五角形や六角形、つまり $n$ 角形に対する知識が深まります。三角形の面積公式の証明 冒頭に述べた球面三角形の面積公式 s = r 2 (a b c − π) s=r^2(abc\pi) s = r 2 (a b c − π) を証明します。 まず二つの大円のなす角が a a a である状況を考えます。二つの大円によって球面は4つに分割されます。

18/8/08 三角形の合同（証明の問題）（高校入試） ネコネコ算数数学ページ がんばってとくにゃ。 三角形の合同（証明の問題）（高校入試） がんばってとくにゃ。 三角形の合同（証明の問2年生 5 図形の性質と証明 どんな三角形でも内角の和は180°であることの証明について，下のアからオまでの中から正しい ものを1つ選びなさい。 ア①も②も証明できている。6/3/21 三角形のその他の中心 実は，三角形は五心以外にも5000種類以上の中心が存在します。 詳しくはEncyclopedia of Triangle Centers参照。 代表的なものをいくつか紹介していきます。 ・フェルマー点 6：三角形のフェルマー点の3通りの証明

三角形の形状問題も，角度に関する式を辺に関する式に直してから考えるのが基本です． a=b など a=b の→二等辺三角形 a 2 =b 2 c 2 など→ ∠A=90° の直角三角形 などど答えます．三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。以下の1～3に示した各組の三角形が相似であることを証明しなさい。 （※辺の長さの単位はcm） 1 ABCと EDC 2 ABCと AED 3 ABCと EBD 練習問題2 右図において、AD∥BCで、2つの線分ACとDB の交点をPとする。 このとき、 ADP ∽ C BPであることを証明し

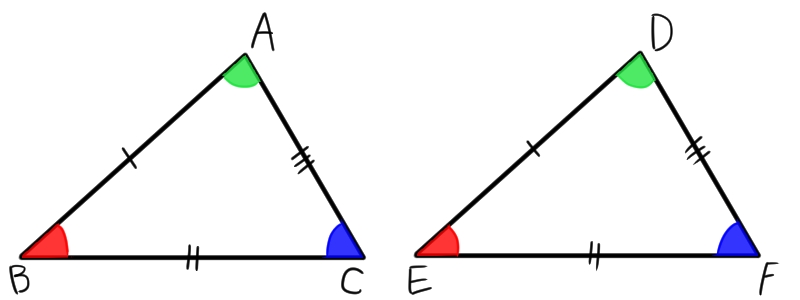
中学2年生の数学 証明 三角形の合同条件と証明の書き方 塾講師が数学をやりmath

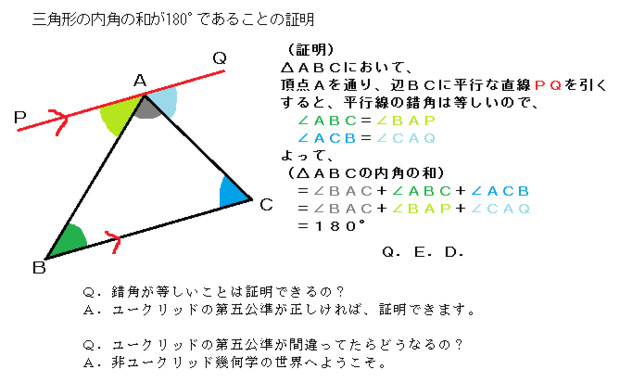
三角形の内角の和が180 であることの証明 キグロ さんのイラスト ニコニコ静画 イラスト

三角形証明 (発展1) 図の ABCはAB=AC,∠BAC=90°の直角二等辺三角形である。 ADEはAD=AE,∠DAE=90°の直角二等辺三角形である。 このときBD=CEを証明しなさい。 A B C D E 次の図のような ABCがある。 辺AC上に点Dがあり、BCの延長上にEがある。 点Dを通り辺BCに平行な直線をnとして、直線nと∠BCAの二等分線との交点をF,直線nと∠ACEの二等分線との交点をGとする。まず証明の簡単な概要について説明します。 図のように三角形の1辺を延長し、さらに1辺と平行な線を引きます。 平行線の錯角・同位角が等しいことから、三角形の内角と等しい角度が外角にできます。 内角の和と等しい角度が1直線に並ぶため180°と等しいことがわかりました。 以上をきちんと証明するには以下のようになります。 三角形の内角の和が180°に6/3/21 つまり， 三角形において，各辺の垂直二等分線は1点で交わる という定理を使います。 証明 三角形 A B C ABC A BC の各頂点を通り対辺と平行な直線を3つ引き，それらの交点を D , E , F D,E,F D , E , F とおく。

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

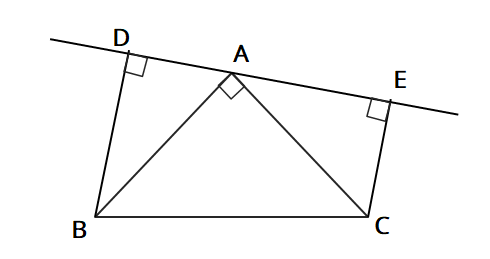
中2数学 直角三角形の合同の証明 応用問題 デルココ

 op = oaよって、 opaはop = oaの二等辺三角形である。 二等辺三角形の底角は等しいから、 ∠oap = ∠opa ・・・ (1)三角形の外角の定理より、 ∠aob = ∠oap ∠opa・・・(2) (1)、(2)より、三角形や四角形の合同証明の問題を苦手としている中学生はたくさんいますね。 図形の証明は高校入試でもよく出るので、しっかりマスターしておきたいところです。 合同証明を克服するための勉強法 を紹介しますので、参考にしてください。6/3/21 三角形の成立条件の証明（必要性） 「三角形が成立する→三角不等式が成立する」を証明します。 寄り道した方が距離が長くなる という直感に従うと自明ですが，一応きちんと証明しておき

Math 平行と合同 直角三角形は 直角でない角に と をつける 働きアリ

Studydoctor三角形の合同の証明 応用 中２数学 Studydoctor

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators傍心の存在証明 三角形の傍心が存在することの証明をします。 「外角の二等分線と対角の二等分線が1点で交わること」がすべての三角形でいえるのかを確かめましょう。 長くなってしまったので証明が気になる方は下をクリックしてください。\(\triangle ABC\) が二等辺三角形であることを証明せよ三角形が二等辺三角形であることを示したいとき、・\(2\) つの辺が等しい・\(2\) つの角が等しいのどちらか片方がいえればOKです。これも暗記ですよ。三角形の合同条件を暗記したの同じように。

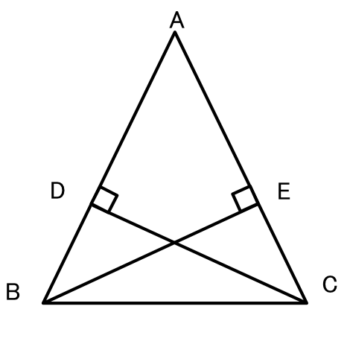
フロー 2 5 4 4 直角三角形の合同条件を利用した証明

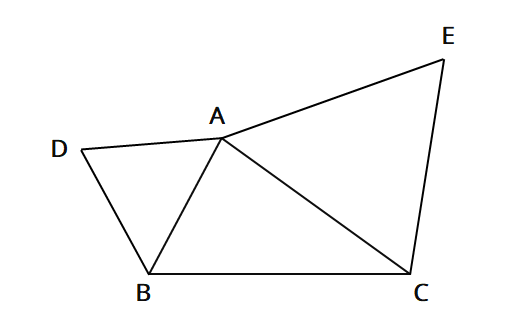
中２数学 三角形の合同の証明応用問題 デルココ

 なぜ、どんな形をした三角形でも、その面積は 「三角形の面積 底辺 高さ 」 「 三 角 形 の 面 積 = 底 辺 × 高 さ ÷ 2 」 で求まるのでしょうか。 形がちがう2種類の「底辺 5 c m 高さ 2 c m の三角形」を通じてみていきましょう。 ※1マス 1 c m 初めに、同じ形定理の証明 ① abcと adeにおいて de//bcより、平行線の同位角は等しいので ∠abc=∠ade, ∠acb=∠aed よって2組の角がそれぞれ等しいので abc∽ ade 相似な三角形の対応する辺の比は等しいので adab=aeac=debc ② f eを通りabと平行な直線をひき、bcとの交点をfとする。証明の手順 を簡単にまとめます。 中2生の皆さんは、 しっかりチェックしましょう。証明の手順 1．仮定を探して書く ↓ 2． 仮定以外 で同じ大きさのものを書く ↓ 3． 「三角形の合同条件」 の3つのうち、どれかを書く ↓ 4．結論を書く

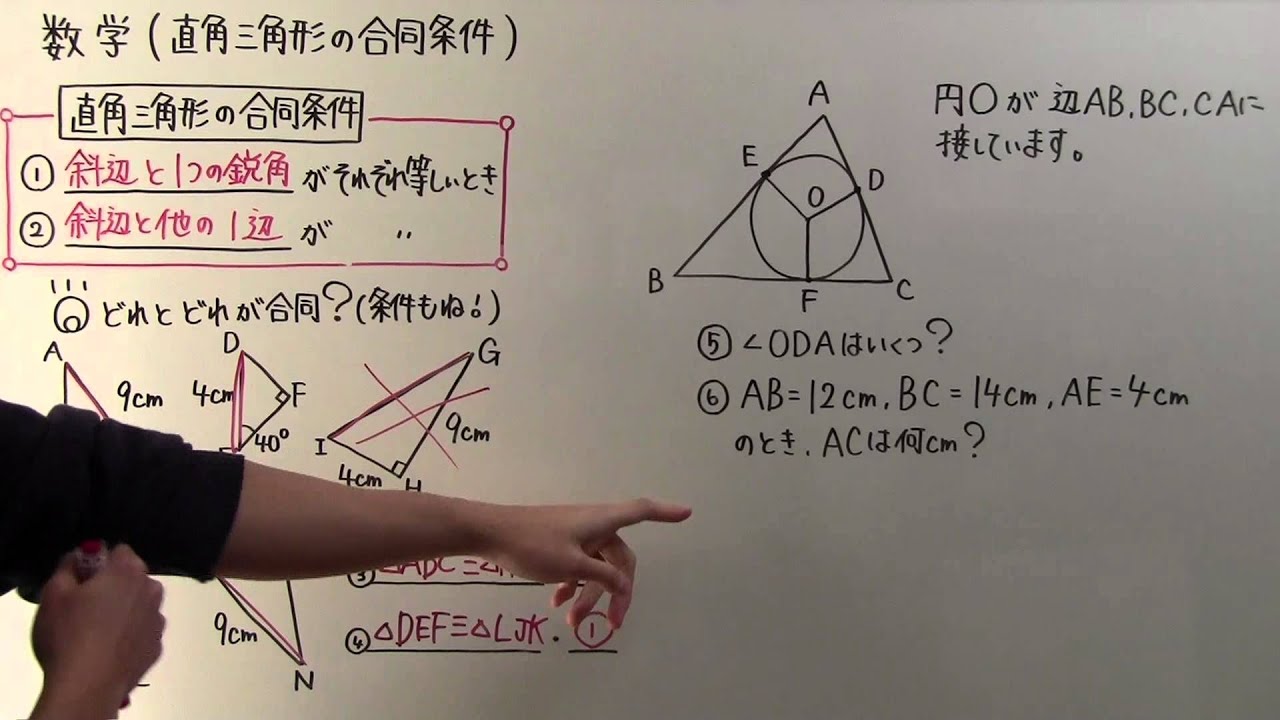
数学 中2 71 直角三角形の合同条件 Youtube

直角三角形と証明 Youtube

 これは、これらの2つの三角形で、Δabcの2つの角度と含まれていない辺がΔzyxの2つの角度と含まれていない辺に合同であることを示しています。 したがって、Δabc≅Δzyx。 aasを使用した別の証明を見てみましょう。 2 与えられた： ea ≅ ec三角形の形状・証明問題 == 《解説》 三角形の形状問題（正三角形，二等辺三角形，直角三角形など三角形の種類を言い当てる問題）や証明問題においては，正弦定理や余弦定理を変形して，角度に関する式を辺に関する式に直してから考えるのが原則です．証明の書き方合同な三角形の証明問題の書き方を基礎から解説！←今回の記事 直角三角形証明問題の書き方とは？合同条件の使い方を徹底解説！ 二等辺三角形の角度の求め方 厳選6問解説！ 正三角形の角度 正方形、ひし形との融合問題を解説！

直角三角形の合同の証明の問題です Clearnote

中２数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾

28/8/21 こちらで 確認してくださいね 中2数学「二等辺三角形と角」の問題 どこよりも簡単な解き方・求め方 今回は、特別な三角形「二等辺三角形」の「定義」「定理」「角の問題」を一緒に見ていきましょう 今回は 二等辺三角形の「証明」 について学習していきましょう 「証明の書き方」は いくつか種類があります 学校でのテストでは5/7/16 中学2年の三角形合同の証明で, 合同であることが証明した後の合同な図形の対応する 角は等しいから・・・・ を 単に したがって とか よって で記述しても 正解でしょうか。 お願いします。中学数学三角形の合同の証明の利用・その1 中学数学三角形の合同の証明の利用・その2 中学数学証明・二等辺三角形の性質の利用 中学数学証明・二等辺三角形であることの証明 中学数学正三角形の性質を利用した証明

三角形の合同条件

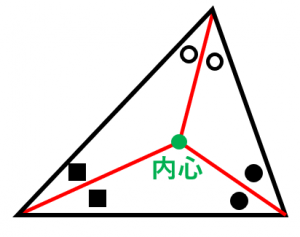
三角形の内心の証明と頻出例題2問 具体例で学ぶ数学

1

三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学

中2数学 三角形の合同を証明する問題 練習編 映像授業のtry It トライイット

中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ

三角形の合同条件を使った証明問題 中学２年生の問題を解こう 身勝手な主張

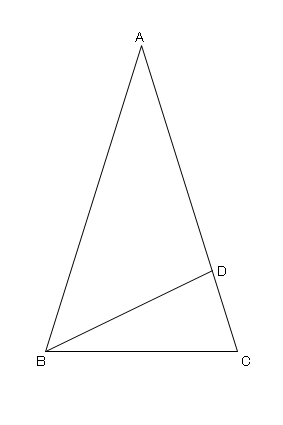
三角形の相似の証明 2 ネット塾

合同の証明 清水塾

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

2

正三角形と証明 中学２年 数学クラブ

この正三角形の証明の仕方を教えてください Clearnote

二等辺三角形に関するある問題 底辺 高さそして面積 身勝手な主張

中2数学 二等辺三角形の証明 練習編 映像授業のtry It トライイット

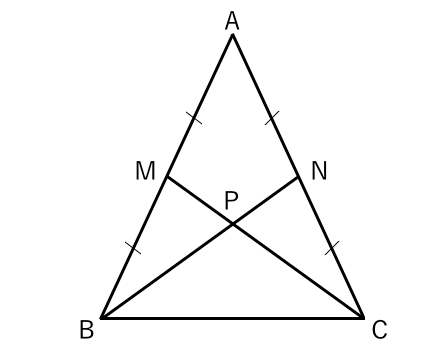
合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に

三角形の合同条件

中学数学が秒でわかる 正三角形の中に正三角形がある図形の証明 超 解説付き なぜか分かる はかせちゃんの怪しい研究室

3

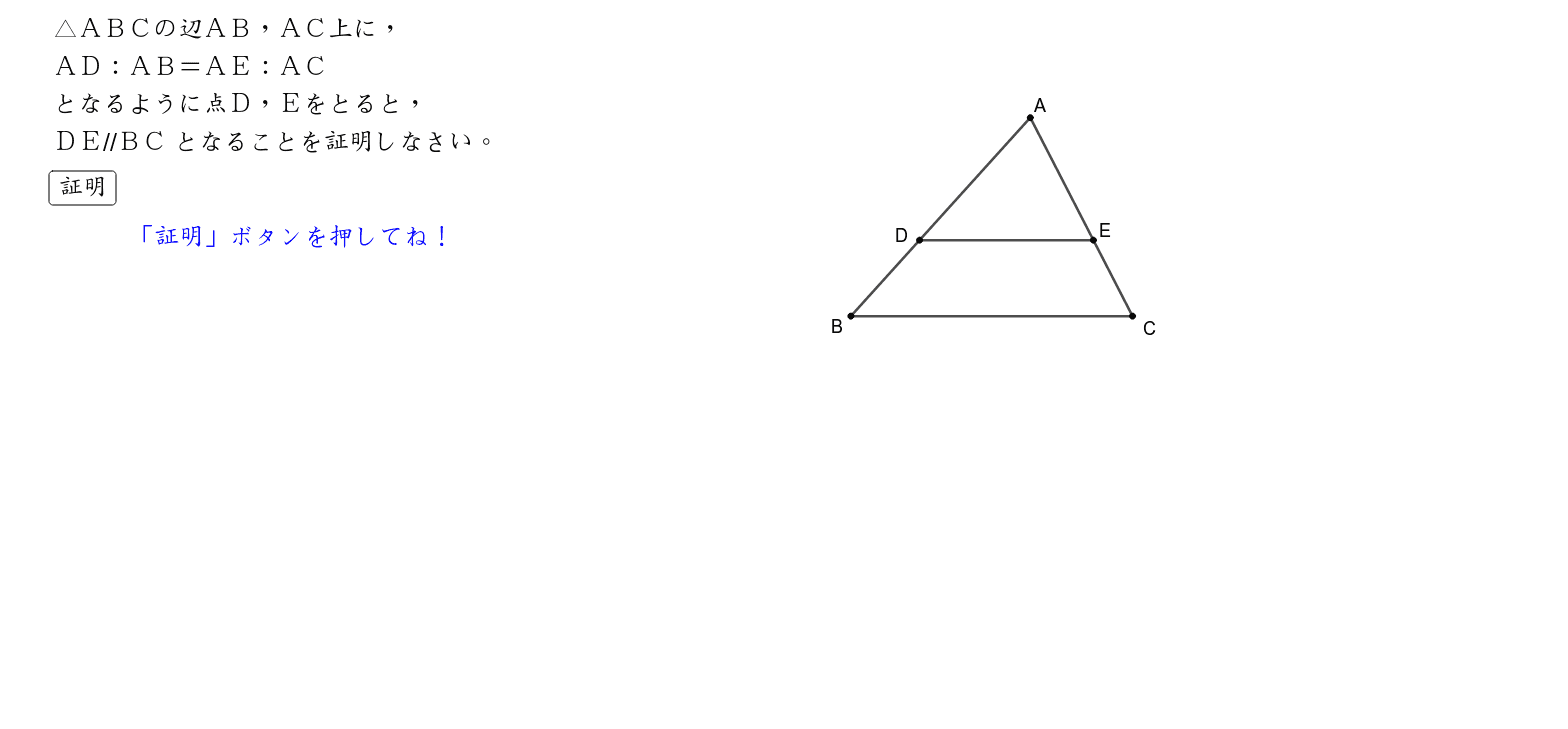
三角形と比の逆の証明 Geogebra

合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典

中学2年生の数学 証明 二等辺三角形と直角三角形 塾講師が数学をやりmath

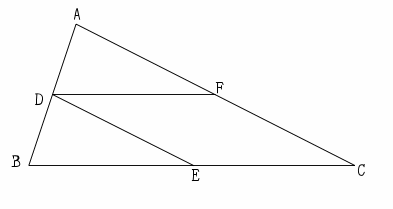
合同の証明2

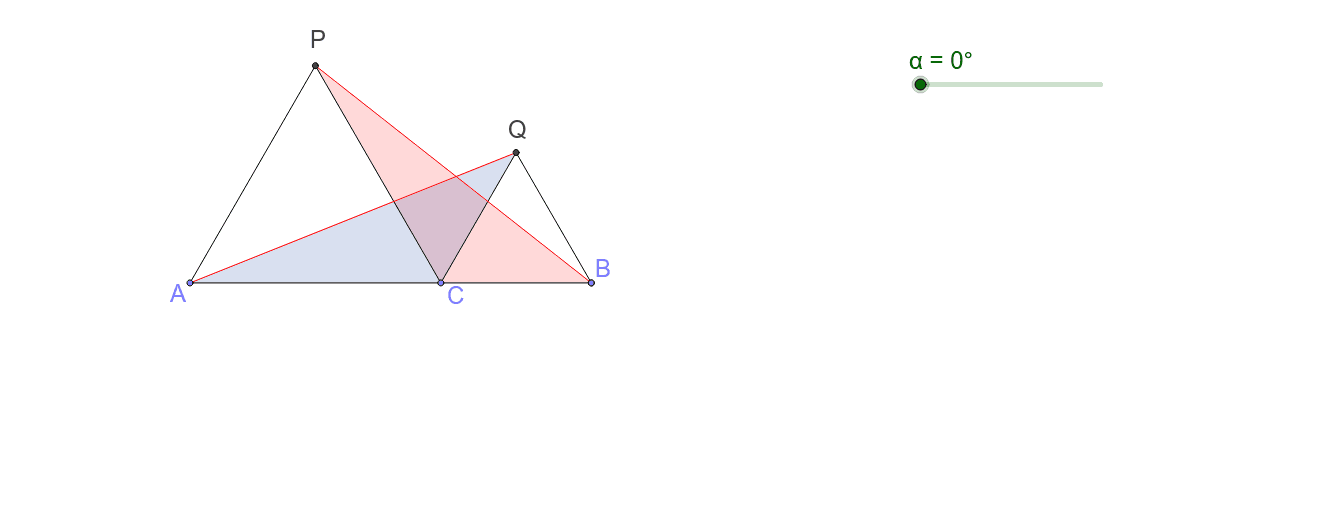
正三角形と合同 Geogebra

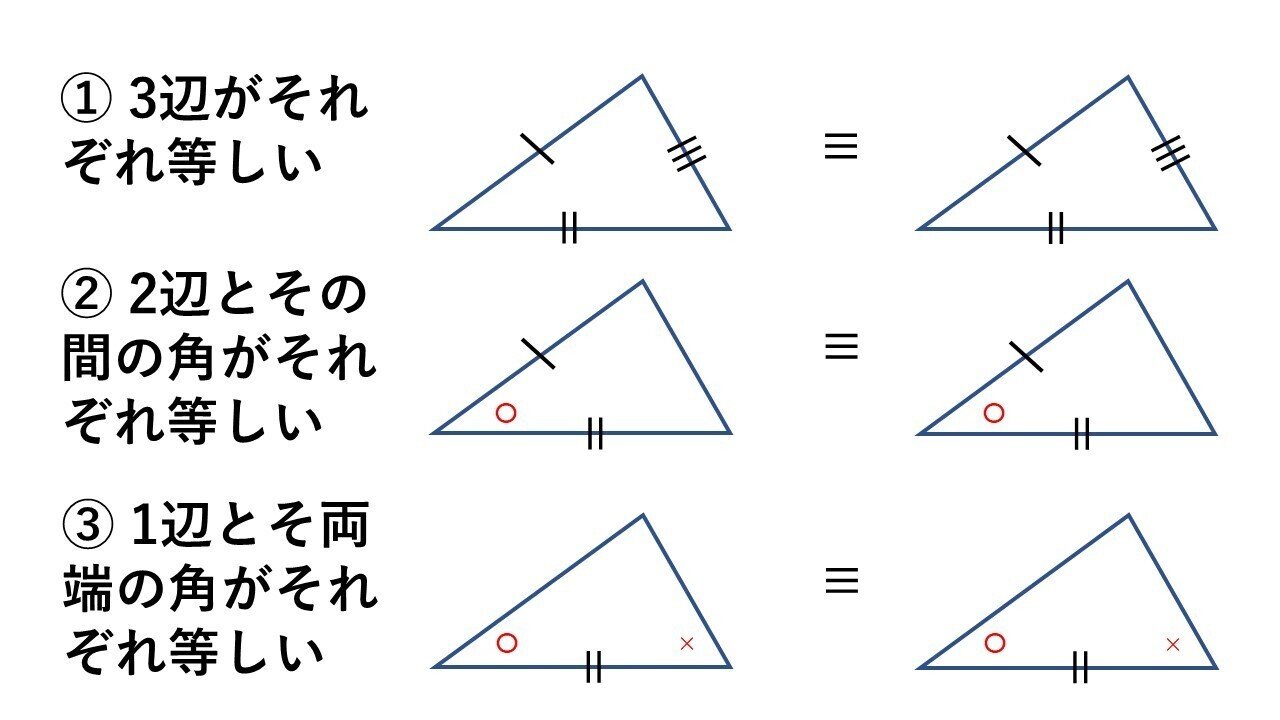
三角形の合同条件から証明へ タロウ岩井の数学 Note

二等辺三角形になることの証明 Youtube

中学数学 証明は簡単 合同な図形を探すたった1つのポイント 烈志塾 塾長ブログ

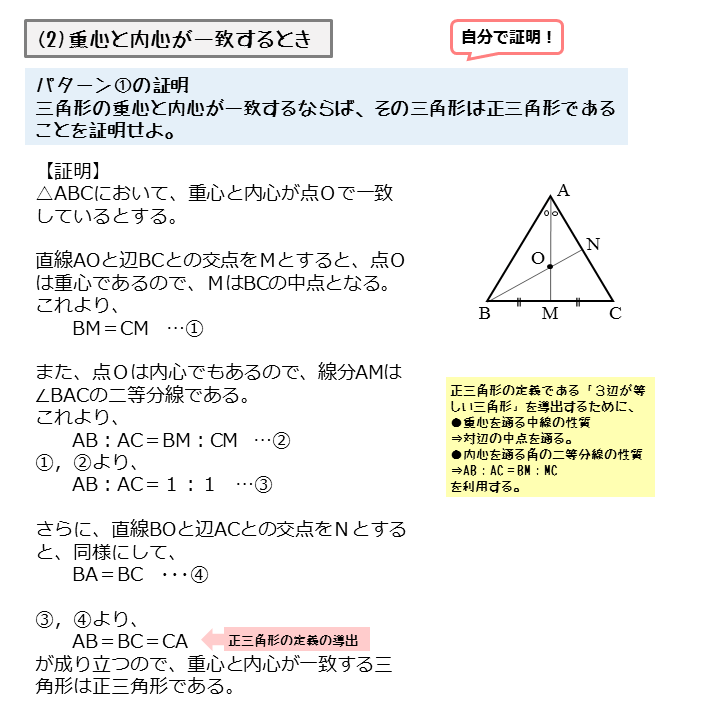
図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん

2 61 第４章 直角三角形 直角三角形と証明 1 中学生

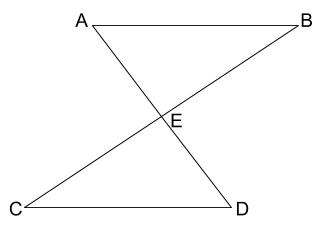
中学数学 三角形の合同の証明 その１ 中学数学の無料オンライン学習サイトchu Su

二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学

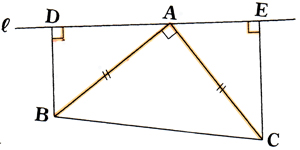
直角三角形の合同証明 難 の解説 春日井市高蔵寺の学習塾 西村セミナールーム

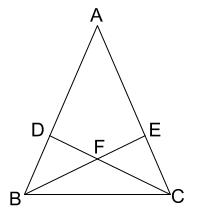
中学数学 証明 二等辺三角形であることの証明 中学数学の無料オンライン学習サイトchu Su

中２数学 証明の基礎 仮定 結論 三角形の合同を利用 まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト

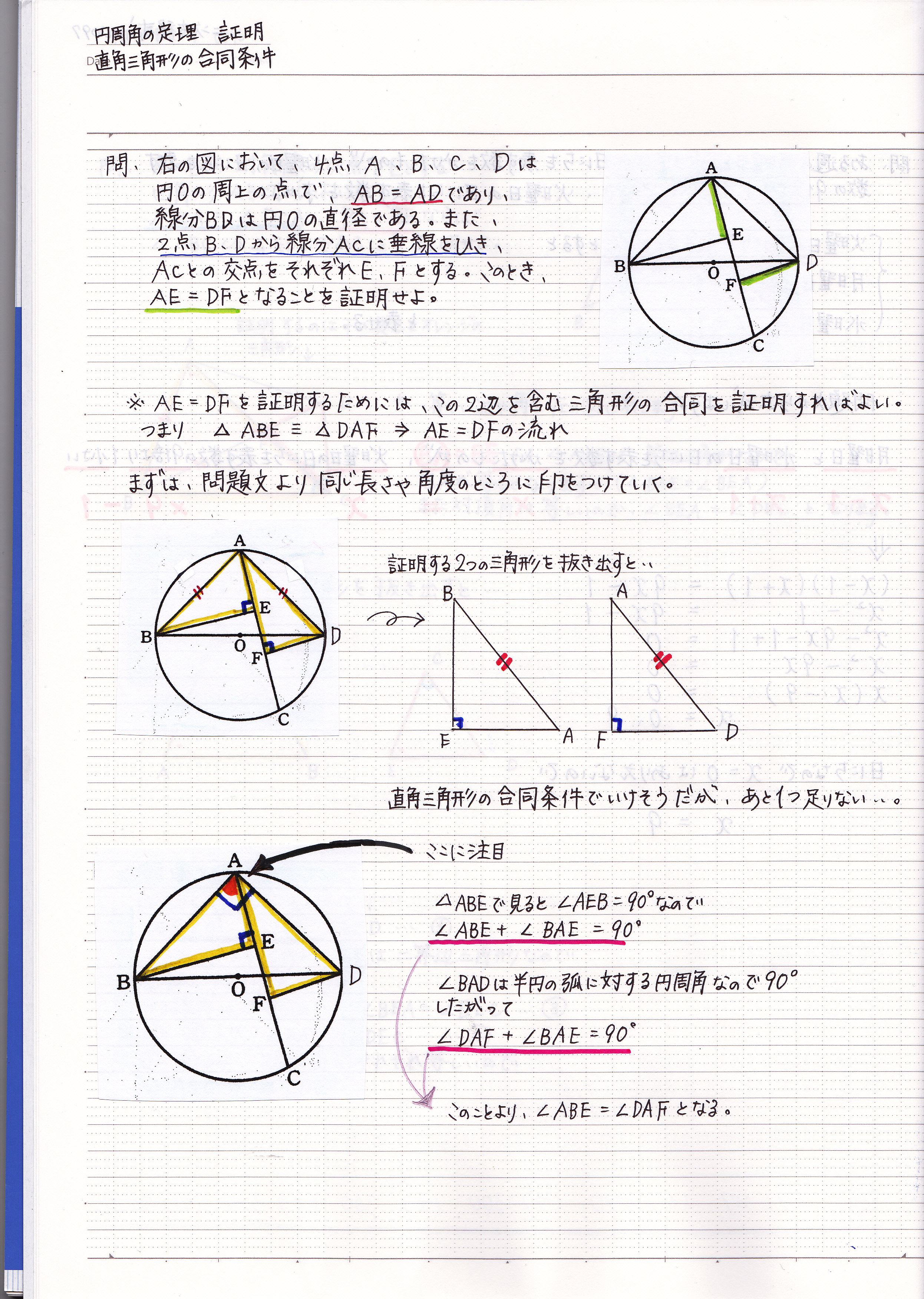
直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方

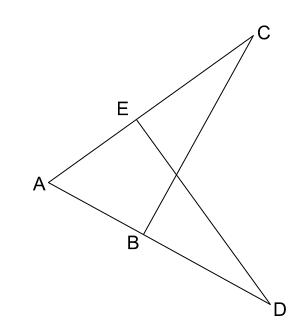
中学数学 三角形の合同の証明 その２ 中学数学の無料オンライン学習サイトchu Su

二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学

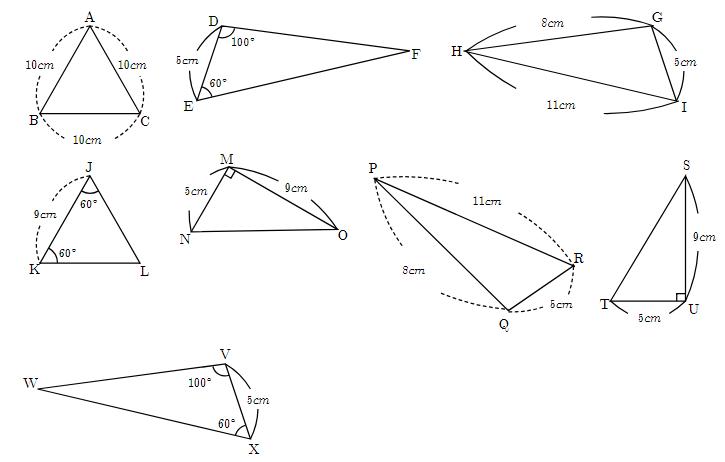
中2数学 三角形の証明の仕方 Pikuu

中2数学 二等辺三角形の証明 例題編 映像授業のtry It トライイット

1

3

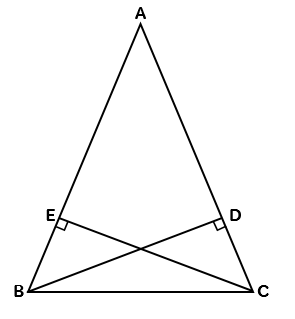
直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ

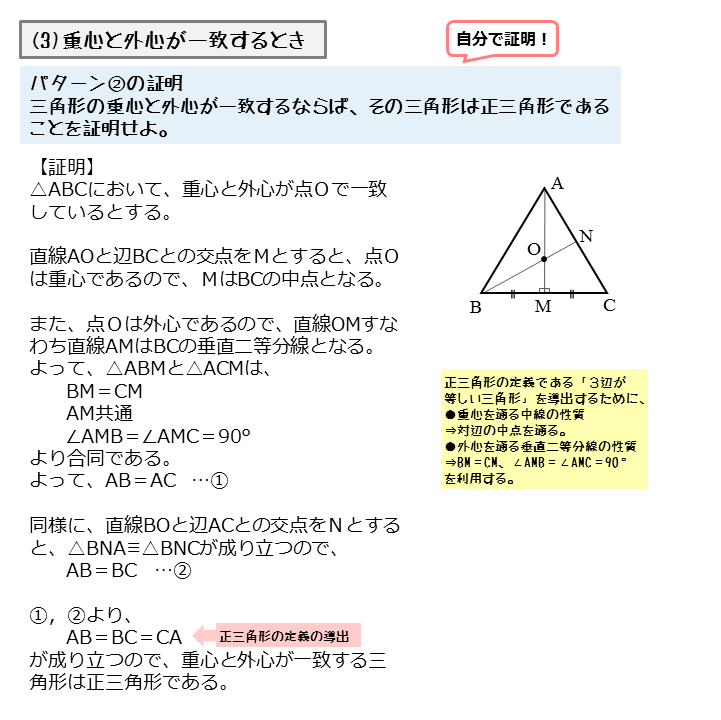
図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん

中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋

世界に一つだけの 三角形ペア 発見 慶大院生２人証明 朝日新聞デジタル

高校数学a 三角形の重心 外心 垂心の位置関係 オイラー線 の幾何的証明 受験の月

直角三角形の合同条件とそれを利用した証明 チーム エン

中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ

二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4

三角形の重心 定義と性質を証明問題と座標を用いる例題で解説 高校生向け受験応援メディア 受験のミカタ

中2 中2 数学 二等辺三角形など 中学生 数学のノート Clearnote

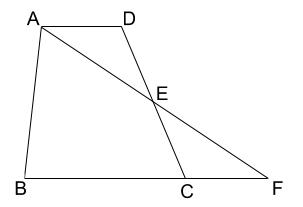
中学数学 三角形の合同の証明の利用 その１ 中学数学の無料オンライン学習サイトchu Su

二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三角形の相似条件と証明問題の解き方 数学fun

二等辺三角形と証明 Youtube

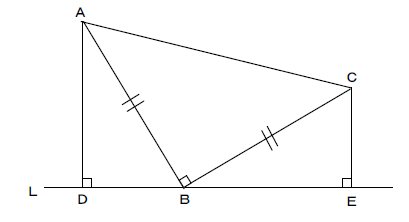
中2数学 直角三角形の合同条件を使った証明の定期テスト過去問分析問題 ダイスト

直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典

超 パワーアップ中学数学 図形の証明 中継点 文字式の表現 活用テクニック Myisbn デザインエッグ社 長通 幸大 本 通販 Amazon

三角形 Ict教材eboard イーボード

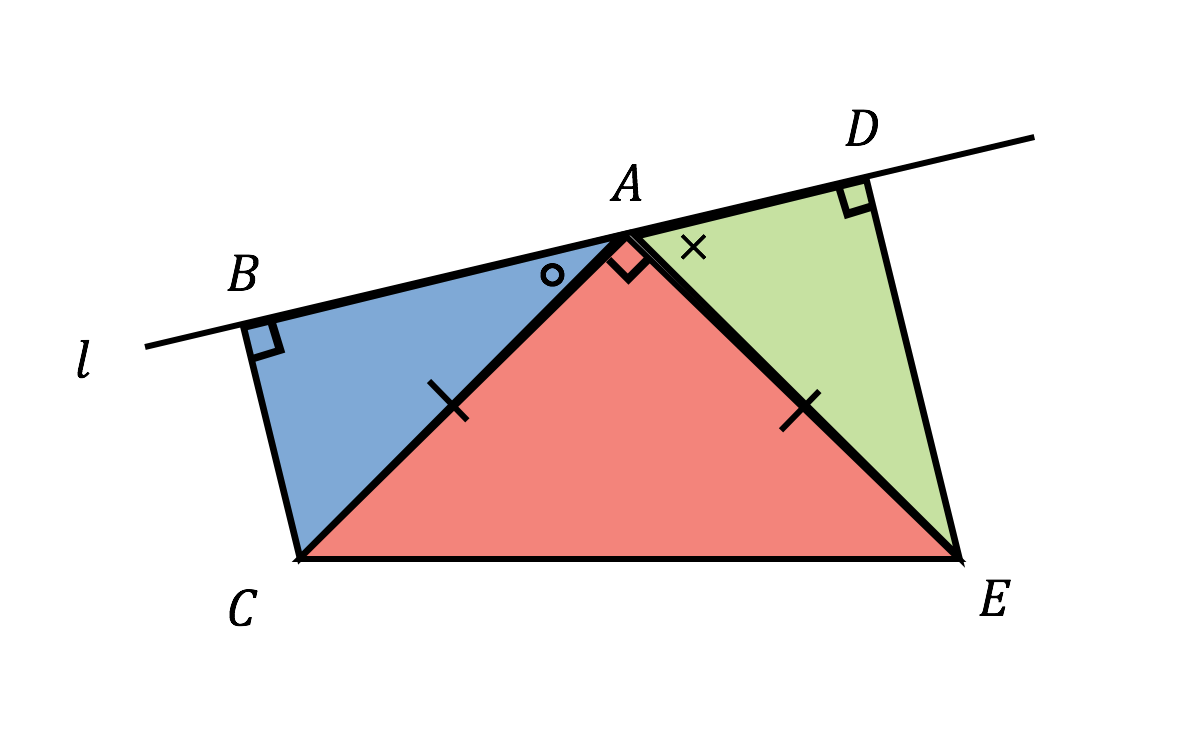
3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ

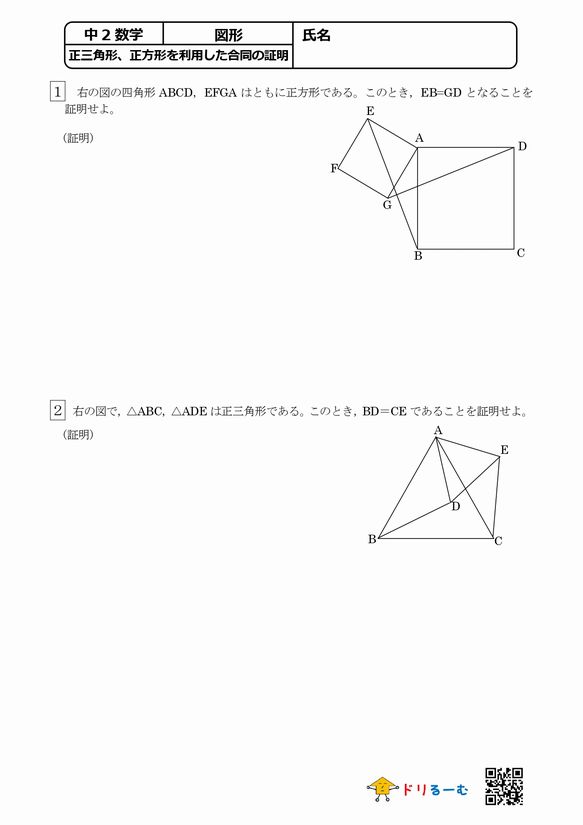
正三角形 正方形を利用した合同の証明 ドリるーむ

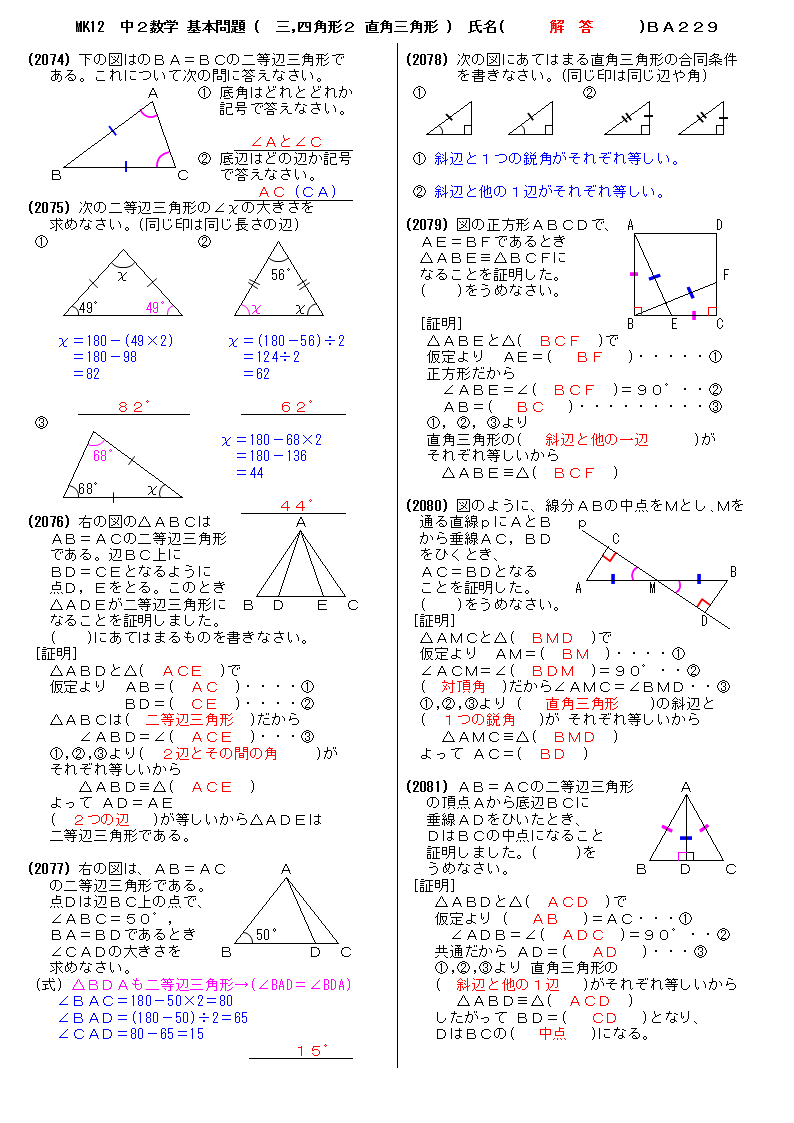
無料 中２数学 基本問題 解答プリント 229 三角形 四角形２ 直角三角形

二等辺三角形の性質を利用した合同の証明 チーム エン

どの三角形の合同を証明すべきか 17年度北海道 高校入試 数学 良問 難問

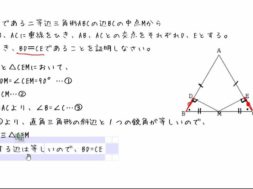
中2数学 08 11 直角三角形を使った証明 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト

三角形の重心の性質とその証明 求め方 数学a By となりがトトロ マナペディア

中2数学 正三角形の証明 練習編 映像授業のtry It トライイット

三角形の合同証明の練習 無料で使える中学学習プリント

合同の証明 清水塾

教材研究 二つの正三角形の問題 2 軌跡の観点からの探究と授業化

三角形の合同の証明問題 中学 時空先生のドリルプリント

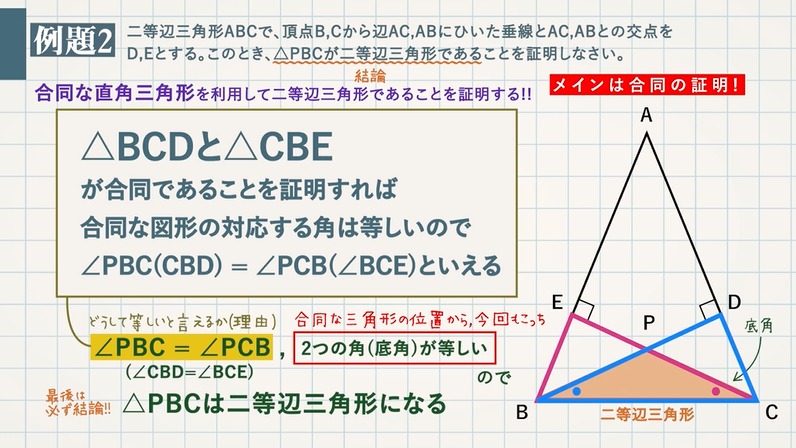
二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

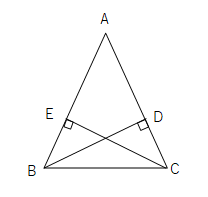
中2数学 直角三角形の合同証明のポイントと練習問題 Examee

二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく

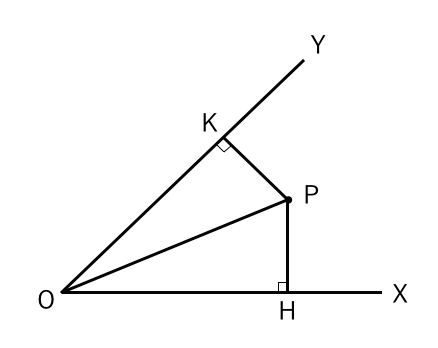
直角三角形の合同 証明問題 苦手な数学を簡単に

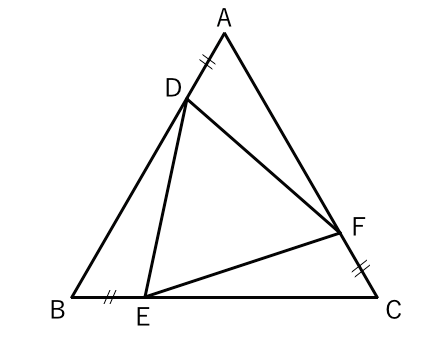
合同な図形 正三角形の証明問題 苦手な数学を簡単に

直角三角形の合同条件とその証明 数学fun

三角形の合同条件と証明問題の解き方 数学fun

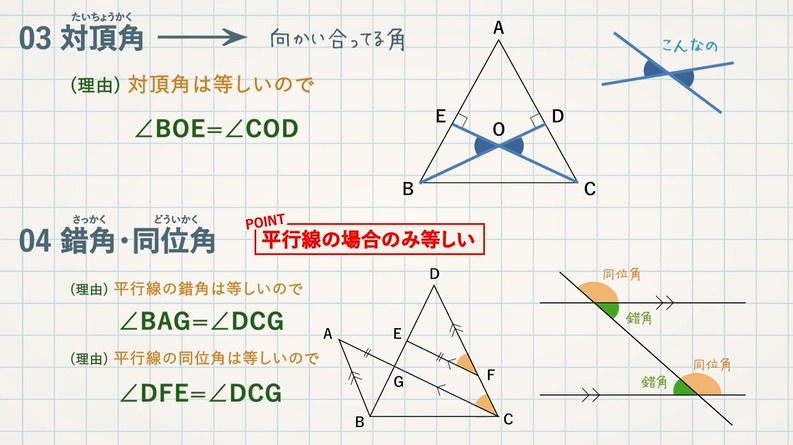
証明 合同 相似 が苦手な人へ 教遊者

中学数学 高校受験chu Su 証明 正三角形 ２ １ 中学数学 数学 中学

中２数学 二等辺三角形の基礎 角の大きさ 二等分線 合同を用いた証明 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト

二等辺三角形になることの証明 Youtube

Studydoctor三角形の合同証明の進め方 中２数学 Studydoctor

三角形の合同条件 合同の証明問題と解き方のコツ リョースケ大学

直角三角形と証明 Youtube

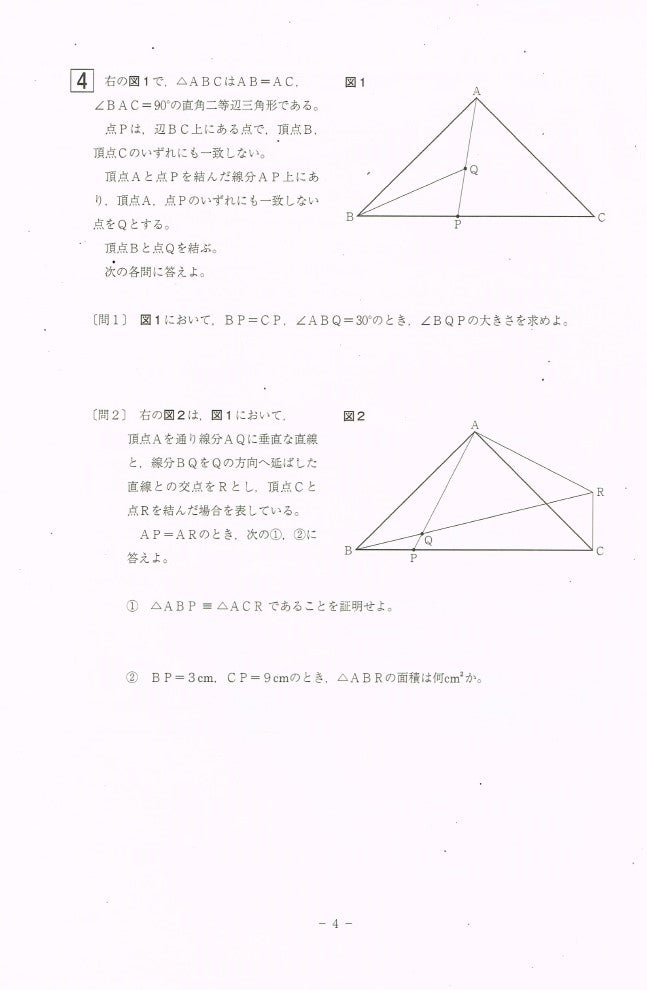
数学の証明問題の解き方 セルモ大蔵 世田谷 の塾長ブログ

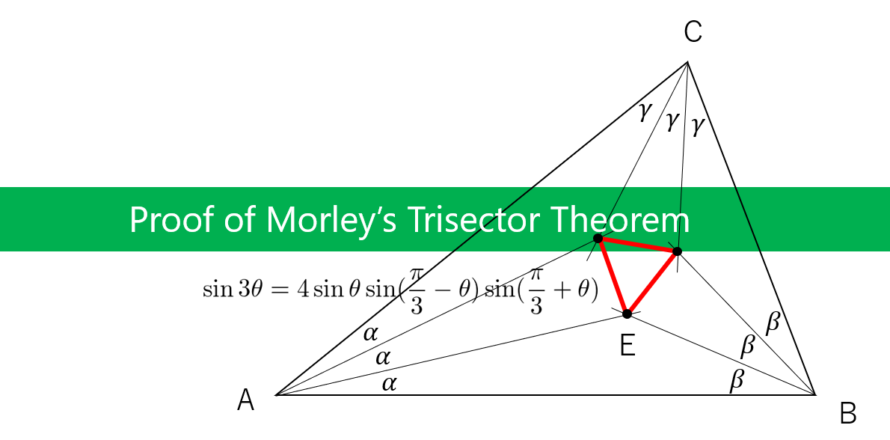
モーリーの定理の証明 三角比を使った方法 数学 統計教室の和から株式会社

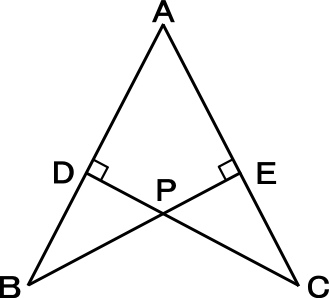
中学２年数学練習問題 図形と合同 三角形の合同の証明問題

高校数学a 三角形の五心 三角形の重心とその存在証明 受験の月

三角形の合同証明の練習 無料で使える中学学習プリント

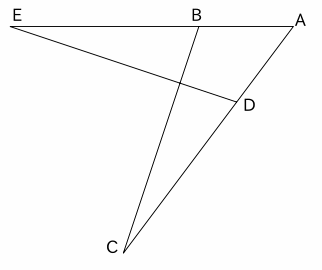
合同の証明6

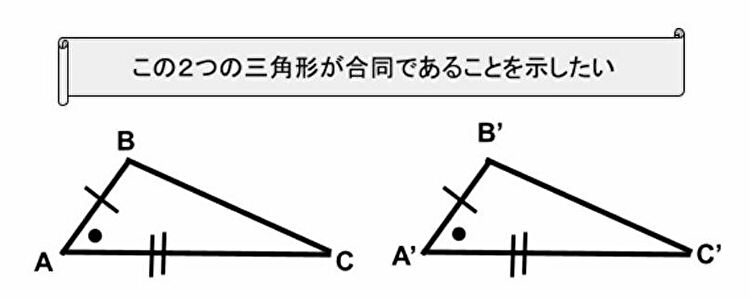
公理から手繰る 三角形の合同条件の証明 二辺挟角 Sas 数学探求 ぱるきちどっとこむ

Incoming Term: 三角形の証明問題中2, 三角形の証明 問題, 三角形の証明 難問, 三角形の証明コツ, 三角形の証明 中2, 三角形の証明 応用, 三角形の証明 プリント, 三角形の証明 ゲーム, 三角形の証明 導入,